‘Geometry’ is a branch of Mathematics dealing with shapes, sizes, orientations and their measurements.

Line segment: A line segment has two end points with a definite length.
Plane
A plane is a 2-dimensional figure which we can extend infinitely and is flat. Therefore, the Plane includes 2D figures like quadrilaterals, triangles and includes areas and perimeters.

Point
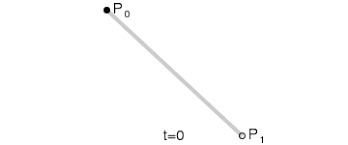
A point is basically a location or a position in space or on a plane. As you can see below, two locations on the given line to are specified by point ‘P0‘ and point ‘P1‘. With reference from an origin, each of these points has a specific location.
Angles
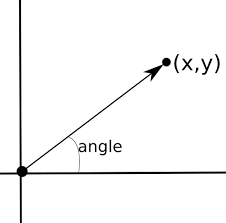
An angle is defined as the inclination of one line with respect to the other at the point of their intersection.
Curve
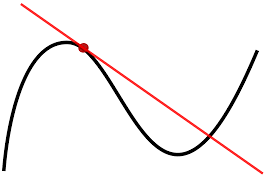
A curve is a 1-dimensional entity which can be a straight line or a curved entity. In other words, a curve is a one-dimensional mathematical entity that may be straight or not! Hence, every line – straight or not can be a curve. Curves may be open – when the endpoints of a curve don’t meet or closed – when the endpoints of the curve meet.
Surface
A surface is a 2D or a 3D construction in space or a plane with no thickness. Therefore, we use it in the calculation of surface area.

Ray: A ray has one end point and infinitely extends in one direction.

Straight line: A straight line has neither starting nor end point and is of infinite length.

Types of lines:
(i) Horizontal lines: The lines drawn horizontally are called horizontal lines.
(ii) Vertical lines: The lines drawn vertically are called vertical lines.
(iii) Oblique or slanting lines: The lines drawn in a slanting position are called oblique or slanting lines.
Acute angle: The angle that is between 0° and 90° is an acute angle, ∠A in the figure below.

Obtuse angle: The angle that is between 90° and 180° is an obtuse angle, ∠B as shown below.

Right angle: The angle that is 90° is a Right angle, ∠C as shown below.

Straight angle: The angle that is 180° is a straight angle, ∠AOB in the figure below.
Supplementary angles:

In the figure above, ∠AOC + ∠COB = ∠AOB = 180°
If the sum of two angles is 180° then the angles are called supplementary angles.
Two right angles always supplement each other.
The pair of adjacent angles whose sum is a straight angle is called a linear pair.
Complementary angles:
Complementary angles:

∠COA + ∠AOB = 90°
If the sum of two angles is 90° then the two angles are called complementary angles.
Adjacent angles:
Adjacent angles:
The angles that have a common arm and a common vertex are called adjacent angles.
In the figure above, ∠BOA and ∠AOC are adjacent angles. Their common arm is OA and common vertex is ‘O’.
Vertically opposite angles:
Vertically opposite angles:
When two lines intersect, the angles formed opposite to each other at the point of intersection (vertex) are called vertically opposite angles.

In the figure above,
x and y are two intersecting lines.
∠A and ∠C make one pair of vertically opposite angles and
∠B and ∠D make another pair of vertically opposite angles.
Pair of lines



Perpendicular lines: When there is a right angle between two lines, the lines are said to be perpendicular to each other.
Pair of lines
Intersecting Lines
A pair of lines, line segments or rays are intersecting if they have a common point. This common point is their point of intersection. For example, two adjacent sides of a sheet of paper, a ruler, a door, a window and letters.

Parallel Lines
If a pair of lines lie in the same plane and do not intersect when produced on either side, then such lines are parallel to each other.
If L and M are two parallel lines, we read it as L is parallel to M. We know that two lines in the same plane either intersect or are parallel to each other. However, these two lines L and M, lying in the same plane are parallel if they do not meet anywhere, however far they are extended.
Note that the distance between two parallel lines is the same everywhere. For example a railway track, opposite sides of a blackboard, two opposite edges of a door etc.
Transversal Lines
A straight line which cuts two or more straight lines at distinct points is called a transversal line. For example, a railway line crossing several other lines. In the figure, t is a transversal line and l, m are parallel lines.

Perpendicular lines: When there is a right angle between two lines, the lines are said to be perpendicular to each other.

Here, the lines OA and OB are said to be perpendicular to each other.
Angle pairs formed by parallel lines cut by a transversal
When two parallel lines are given in a figure, there are two main areas: the interior and the exterior.


When two parallel lines are cut by a third line, the third line is called the transversal.
In the example below, parallel lines m and n are cut by a transversal line, t. Here, m and n are two parallel lines, intersected by a line t.
The line t is called a transversal, that which intersects two or more lines (not necessarily parallel lines) at distinct points.
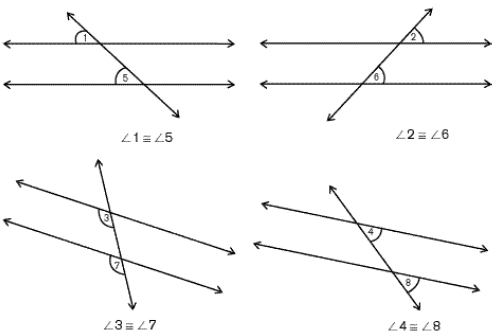
As seen in the figure above, when a transversal intersects two lines, 8 angles are formed.

There are several special pairs of angles formed from this figure. Some pairs have already been reviewed:
Vertical pairs:
∠1 and ∠4
∠2 and ∠3
∠5 and ∠8
∠6 and ∠7
Recall that all pairs of vertical angles are congruent.
Supplementary pairs:
∠1 and ∠2
∠2 and ∠4
∠3 and ∠4
∠1 and ∠3
∠5 and ∠6
∠6 and ∠8
∠7 and ∠8
∠5 and ∠7
Recall that supplementary angles are angles whose angle measure adds up to 180°. All of these supplementary pairs are linear pairs. There are other supplementary pairs described in the shortcut later in this section. There are three other special pairs of angles. These pairs are congruent pairs.
Vertical pairs:
∠1 and ∠4
∠2 and ∠3
∠5 and ∠8
∠6 and ∠7
Recall that all pairs of vertical angles are congruent.
Supplementary pairs:
∠1 and ∠2
∠2 and ∠4
∠3 and ∠4
∠1 and ∠3
∠5 and ∠6
∠6 and ∠8
∠7 and ∠8
∠5 and ∠7
Recall that supplementary angles are angles whose angle measure adds up to 180°. All of these supplementary pairs are linear pairs. There are other supplementary pairs described in the shortcut later in this section. There are three other special pairs of angles. These pairs are congruent pairs.
Alternate interior angles two angles in the interior of the parallel lines, and on opposite (alternate) sides of the transversal. Alternate interior angles are non-adjacent and congruent.
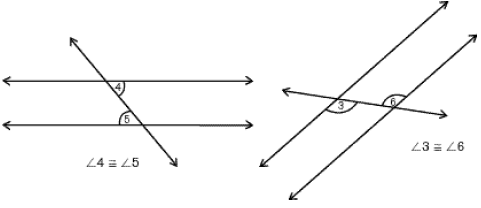

Alternate exterior angles two angles in the exterior of the parallel lines, and on opposite (alternate) sides of the transversal. Alternate exterior angles are non-adjacent and congruent.
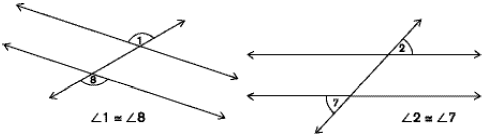
Corresponding angles two angles, one in the interior and one in the exterior, that are on the same side of the transversal. Corresponding angles are non-adjacent and congruent.
Let us consider the details in a tabular form for easy reference.
| Types of Angles | Angles |
| Interior Angles | ∠3, ∠4, ∠5, ∠6 |
| Exterior Angles | ∠1, ∠2, ∠7, ∠8 |
| Vertically opposite Angles | (∠1, ∠3), (∠2, ∠4), (∠5, ∠7), (∠6, ∠8) |
| Corresponding Angles | (∠1, ∠5), (∠2, ∠6), (∠3, ∠7), (∠4, ∠8) |
| Interior Alternate Angles | (∠3, ∠5), (∠4, ∠6) |
| Exterior Alternate Angles | (∠1, ∠7), (∠2, ∠8) |
| Interior Angles on the same side of transversal | (∠3, ∠6), (∠4, ∠5) |
When a transversal intersects two parallel lines,
- The corresponding angles are equal.
- The vertically opposite angles are equal.
- The alternate interior angles are equal.
- The alternate exterior angles are equal.
- The pair of interior angles on the same side of the transversal is supplementary.
We can say that the lines are parallel if we can verify at least one of the aforementioned conditions.





No comments:
Post a Comment