A triangle is a closed figure made up of three line segments.

A triangle consists of three line segments and three angles. In the figure above, AB, BC, CA are the three line segments and ∠A, ∠B, ∠C are the three angles.
Triangles classified by their sides:
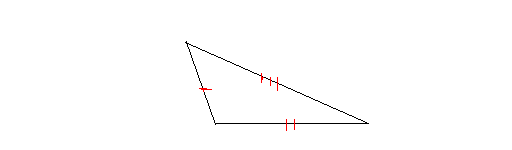
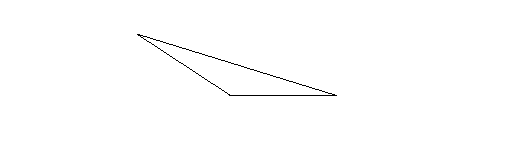
Scalene triangle: A scalene triangle is a triangle that has no equal sides. The following is a scalene triangle.
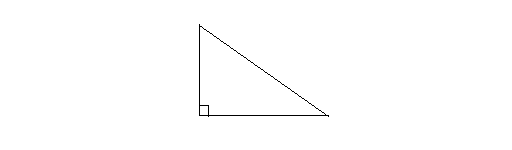
Right triangle: A right triangle has a 90 degrees angle.The following is a right triangle.
If a triangle has one right angle and two equal sides, we can call that triangle right isosceles triangle.
If a triangle has only acute angles and no equal sides, we can call that triangle acute scalene triangle.
If a triangle has two equal sides and one obtuse angle, we can call that triangle obtuse isosceles triangle.
Notice that an angle cannot be obtuse and equilateral at the same time. An equilateral triangle cannot have an obtuse angle because all 3 angles in an equilateral triangle measure 60 degrees.
Basic properties of triangles
- The sum of the angles in a triangle is 180°. This is called the angle-sum property.
- The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Similarly, the difference between the lengths of any two sides of a triangle is less than the length of the third side.
- The square of the hypotenuse of a right triangle is equal to the sum of the squares on the other two sides.
- The side opposite to the largest angle is the longest side of the triangle and the side opposite to the smallest angle is the shortest side of the triangle.

In the figure above, ∠B is the largest angle and the side opposite to it (hypotenuse), is the largest side of the triangle.

In the figure above, ∠A is the largest angle and the side opposite to it, BC is the largest side of the triangle.
Similarity and Congruency in Triangles
Figures with same size and shape are congruent figures. If two shapes are congruent, they remain congruent even if they are moved or rotated. The shapes would also remain congruent if we reflect the shapes by producing mirror images. Two geometrical shapes are congruent if they cover each other exactly.
Figures with same shape but with proportional sizes are similar figures. They remain similar even if they are moved or rotated.
Similarity of triangles
Two triangles are said to be similar if the corresponding angles of two triangles are congruent and lengths of corresponding sides are proportional.
It is written as ∆ ABC ∼ ∆ XYZ and said as ∆ ABC ‘is similar to’ ∆ XYZ.

Here, ∠A = ∠X, ∠B =∠Y and ∠C = ∠Z AND
AB / XY = BC / YZ = CA / ZX
The necessary and sufficient conditions for two triangles to be similar are as follows:
(1) Side-Side-Side (SSS) criterion for similarity:
(1) Side-Side-Side (SSS) criterion for similarity:
If three sides of a triangle are proportional to the corresponding three sides of another triangle then the triangles are said to be similar.

Here, ∆ PQR ∼ ∆ DEF as
PQ / DE = QR / EF = RP / FD
(2) Side-Angle-Side (SAS) criterion for similarity:
(2) Side-Angle-Side (SAS) criterion for similarity:
If the corresponding two sides of the two triangles are proportional and one included angle is equal to the corresponding included angle of another triangle then the triangles are similar.

Here, ∆ LMN ∼ ∆ QRS in which
∠L = ∠Q
QS / LN = QR / LM
(3) Angle-Angle-Angle (AAA) criterion for similarity:
If the three corresponding angles of the two triangles are equal then the two triangles are similar.

Here ∆ TUV ∼ ∆ PQR as
∠T = ∠P, ∠U = ∠Q and ∠V = ∠R
Congruency of triangles
Two triangles are said to be congruent if all the sides of one triangle are equal to the corresponding sides of another triangle and the corresponding angles are equal.
It is written as ∆ ABC ≅ ∆ XYZ and said as ∆ ABC ‘is congruent to’ ∆ XYZ.

The necessary and sufficient conditions for two triangles to be congruent are as follows:
(1) Side-Side-Side (SSS) criterion for congruence:
(1) Side-Side-Side (SSS) criterion for congruence:
If three sides of a triangle are equal to the corresponding three sides of another triangle then the triangles are said to be congruent.

Here, ∆ ABC ≅ ∆ XYZ as AB = XY, BC = YZ and AC = XZ.
(2) Side-Angle-Side (SAS) criterion for congruence:
(2) Side-Angle-Side (SAS) criterion for congruence:
If two sides and the angle included between the two sides of a triangle are equal to the corresponding two sides and the included angle of another triangle, then the triangles are congruent.

Here, ∆ ABC ≅ ∆ XYZ as AB = XY, ∠A = ∠X and AC = XZ.
(3) Angle-Side-Angle (ASA) criterion for congruence: If two angles and the included side of a triangle are equal to the corresponding two angles and the included side of another triangle then the triangles are congruent.
(3) Angle-Side-Angle (ASA) criterion for congruence: If two angles and the included side of a triangle are equal to the corresponding two angles and the included side of another triangle then the triangles are congruent.

In the figure above, ∆ ABD ≅ ∆ CBD in which
∠ABD = ∠CBD, AB = CB and ∠ADB = ∠CDB.
(4) Right-Angle Hypotenuse criterion of congruence: If the hypotenuse and one side of a right-angled triangle are equal to the corresponding hypotenuse and side of another right-angled triangle, then the triangles are congruent.
(4) Right-Angle Hypotenuse criterion of congruence: If the hypotenuse and one side of a right-angled triangle are equal to the corresponding hypotenuse and side of another right-angled triangle, then the triangles are congruent.

Here, ∠B = ∠Y = 90° and AB = XY, AC = XZ.
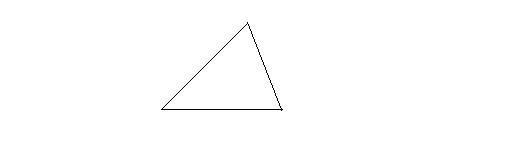





No comments:
Post a Comment