The branch of mathematics which involves variables as numbers is known as algebra.
Rules of Algebra
Here, are some of the definition that will give you a better clarity on this:
Variables
The major point of difference between arithmetic and algebra is the variable. Commonly, the variables are used in the formulas. For example, the area of the triangle is ½ b × h. Here, b represents the base of the triangle and h represents the height of the triangle. ½ used in this formula is a constant. Unlike a variable, a constant is a quantity that remains same throughout and is usually a number.
Expression
An expression is a mathematical phrase which comprises a series of mathematical symbols. These symbols can be operations, variables, and numbers. So, an example of an expression is ½ b × h.
Building of The Algebraic Expressions
The two prime building blocks of an algebraic expression are constants and variables. Any algebraic expression is created with a combination of variables and numbers using the arithmetic operations like subtraction, addition, division, multiplication, and exponentiation.
The term can either be a variable, a number or a product of a variable and number with an exponent. Number part of this term is known as the coefficient. The coefficient can be any real number even 0. In case a variable has no exponent, it still has an exponent 1.
Factors of a term
We saw above that the expression (4x2 – 3xy) consists of two terms 4x2 and –3xy. The term 4x2 is a product of 4, x and x; we say that 4, x and x are the factors of the term 4x2. A term is a product of its factors. The term –3xy is a product of the factors –3, x and y.
We can represent the terms and factors of the terms of an expression conveniently and elegantly by a tree diagram. The tree for the expression (4x2 – 3xy) is as shown in the adjacent figure.
The factors are such that they cannot be further factorised. Thus we do not write 5xy as 5 × xy, because xy can be further factorised. Similarly, if x3were a term, it would be written as x × x × x and not x2× x. Also, remember that 1 is not taken as a separate factor
like terms : Terms that have the same variables and powers. The coefficients do not need to match.
Unlike terms are two or more terms that are not like terms, i.e. they do not have the same variables or powers.
Types of Polynomials:
- Monomials – Monomials are the algebraic expression with one term, hence the name says “Mono”mial.For example: 2x, 4t, 21x2y, 9pq etc. Each of these expressions is monomial since they contain only one term.
- Binomials – Binomials are the algebraic expression with two unlike terms, hence the name “Bi”nomial.For example, 3x + 4x2 is binomial since it contains two unlike terms, that is, 3x and 4x2
- Trinomials – Trinomials are the algebraic expression with three unlike terms, hence the name “Tri”nomial.For example- 3x + 5x2 – 6x3 is an active Trinomial. It is due to the presence of three, unlike terms, namely, 3x, 5x2and 6x3
Polynomial
In simple terms, polynomials are expressions comprising a sum of terms, where each term holding a variable or variables is elevated to a power and further multiplied by a coefficient. The simplest polynomials hold one variable.
Polynomial equation of degree ‘n’ acquires the following form:
anxn + an-1xn-1 + … + a2x2 + a1x + a = 0
Degree of a polynomial
It is simply the greatest of the exponents or powers over the various terms present in the polynomial equation.
Example: the degree of a polynomial 2x – 5 is 1 as highest power of variable is 1.
- Zero Polynomial: Whenever in a given polynomial every coefficient value stays zero, then it is called as a zero polynomial. For example: 4
Addition of polynomials
When adding polynomials, like terms must be combined. For instance, 3c and 5c can be added to get 8c. Likewise, 3x2y and -7x2y can be added to get -4x2y. However, 5x3y and 10x2y5 cannot be added together because they do not have the same exact variables and the exact powers on those variables.
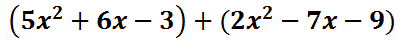
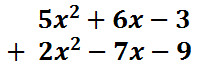
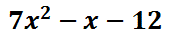
Subtraction of polynomials
When subtracting numbers, it is possible to change the problem to addition. Here is a case in point.
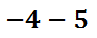
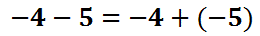
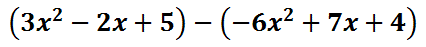
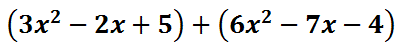
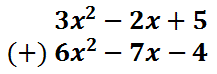
Let those examples guide us regarding the following problem.
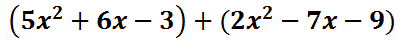
The best way to handle this is to perform the task vertically, instead of horizontally, while aligning like terms.
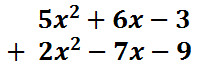
With this arrangement of polynomials, it's easier to determine which terms to combine together.
Consequently, here is the solution.
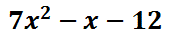
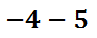
This problem can be changed to an addition problem. All we have to do is switch the subtraction to addition and then change the second number to its opposite, like this.
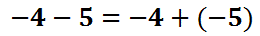
When problems are converted into addition, they are usually done more successfully. The answer is -9, which is harder to obtain as a subtraction problem. When dealing with polynomial subtraction, we can do the exact same process. Here is an example of a subtraction problem with polynomials.
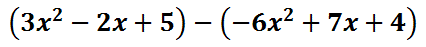
We can also change this problem to addition. Change the subtraction to addition and then switch the last polynomial to its opposite. Our new example would then be…
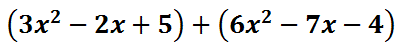
Notice how the second polynomial changed. The -6 changed to 6. The 7 changed to -7 and the 4 changed to -4. Now, the problem is a polynomial addition problem, which is best accomplished vertically.
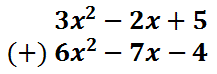
The answer can be gained by adding like terms. The like terms are those that have the same variables and powers on those variables. This vertical form makes it easier to find and add those like terms.
Combining those highlighted like terms gives us the following solution.
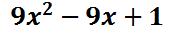
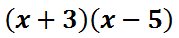
To do this, we will place the first polynomial on the top of our table and the second on the side of our table. [Some people use the method called “FOIL” instead. However, “FOIL” only works for binomials and is useless for other types of polynomial multiplication problems.]
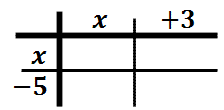
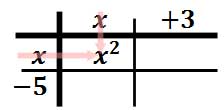
Now, we will multiply a column times a row. We will multiply “x” times “x” and get x2 and then place that in the table.
Likewise, we will multiply “x” times “-5” to get -5x. We will put that in the table.
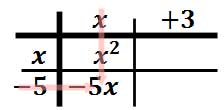
For our last column, we will begin by multiplying "3" times "x." The result is this.
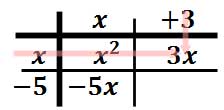
The last item of the table is gained by multiplying "-5" times "3."
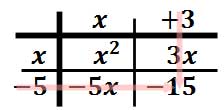
This leaves us with the following table of elements.
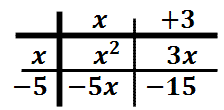
This process has left us with four terms inside the table.
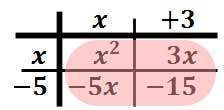
There are two elements within the table that are like terms and they need to be combined together. These are the two like terms.
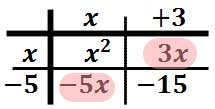
If we write out these four elements horizontally, we get this polynomial.
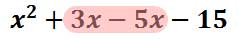
We need to combine the inner-most terms, which are the like terms. After adding the "3x" and the "-5x," we get this solution.
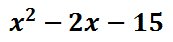
Find the quotient and the remainder of the division of  the dividend, by
the dividend, by  the divisor.
the divisor.
The dividend is first rewritten like this:
The quotient and remainder can then be determined as follows:
- Divide the first term of the dividend by the highest term of the divisor (meaning the one with the highest power of x, which in this case is x). Place the result above the bar (x3 ÷ x = x2).
- Multiply the divisor by the result just obtained (the first term of the eventual quotient). Write the result under the first two terms of the dividend (x2 · (x − 3) = x3 − 3x2).
- Subtract the product just obtained from the appropriate terms of the original dividend (being careful that subtracting something having a minus sign is equivalent to adding something having a plus sign), and write the result underneath ((x3 − 2x2) − (x3 − 3x2) = −2x2 + 3x2 = x2). Then, "bring down" the next term from the dividend.
- Repeat the previous three steps, except this time use the two terms that have just been written as the dividend.
- Repeat step 4. This time, there is nothing to "pull down".
The polynomial above the bar is the quotient q(x), and the number left over ( 5) is the remainder r(x).