How to calculate HCF and LCM?|full form of LCM and HCF
HCF
The HCF or Highest Common Factor of two or more numbers is the greatest common factor of the given set of numbers. In other words, HCF is the greatest number which exactly divides two or more given numbers.
Methods to find HCF
- By listing factors
Factors of 4 are 1,2,4
Factors of 6 are 1,2,3,6
The highest common factor is 2,clearly.
- By prime factorisation
Step 1: Finding prime factors individually:

- All possible factors of 36 are: 2×2×3×3×1
- All possible factors of 48 are: 2×2×2×2×3×1
Step 2: Choose out the common factors: 2×2×3
Step 3: Multiply all the common factors to get the HCF of the given numbers:
Here the given numbers are 36 and 48. The product of the common factors: 2×2×3 = 12. So the HCF for the numbers 36 and 48 is 12.
- By division or Euclid's division algorithm
To find the H.C.F. of the given number we will follow the following steps:
- We divide the bigger number by smaller one.
- Divide smaller number in step 1 with remainder obtained in step 1.
- Divide divisor of second step with remainder obtained in step 2.
- We will continue this process till we get remainder zero and divisor obtained in end is the required H.C.F.
Let’s take few examples for this:
Example : Find the H.C.F. of 248 and 492?
To find the solution we will follow the following method i.e. we divide bigger number 492 by smaller one i.e. 248
So the divisor in the end was 4 so the H.C.F of the given numbers is 4
LCM
The least common multiple (LCM) of two numbers is the smallest number (not zero) that is a multiple of both.
Methods to find LCM are
- By prime factorisation :First we find the prime factors of the given numbers.
12 = 2 × 2 × 316 = 2 × 2 × 2 × 224 = 2 × 2 × 2 × 2 × 3(2 comes maximum 4 times and 3 comes maximum once only.)L.C.M. = 2 × 2 × 2 × 2 × 3= 48 which is the product of their prime factors.
- By division-We can also find the L.C.M. of the given numbers by dividing all the numbers at the same time by a number that divides at least two of the given numbers.
1. When a number is not exactly divisible, we write the number itself below the line.2. When we cannot divide the numbers by a common factor exactly we discontinue dividing the numbers.L.C.M. = 2 × 2 × 2 × 3 × 2 = 48


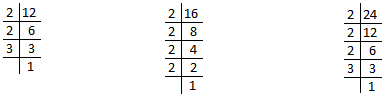




No comments:
Post a Comment